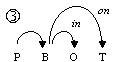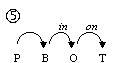Abstract*
A statistical method of disambiguation in text analysis is proposed. The method is based on the statistics of errors that a specific parser used for text analysis makes on a specific types of documents. For each phrase, a weight (or probability) of each variant is determined basing on the statistics of the features (constructions; in our case, subcategorization frames) in the language and in the wrong variants generated by the specific parser; the variant with the largest weight is considered the best. The method probably can be applied to syntactic disambiguation, part of speech tagging, and similar tasks.
Key words: Natural language processing, statistical text analysis, ambiguity resolution, syntactic analysis, prepositional phrase attachment.
Once
having lied, who will trust you?
Koz¢ma Prutkov,
a Russian philosopher.
1. Introduction: Ambiguity of prepositional phrase attachment
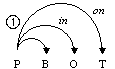
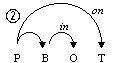
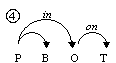
One of the most difficult problems of natural language processing is ambiguity, especially syntactic ambiguity. Let us consider a simple English phrase: How to put the block in the box on the table[1]. The morphological representation of this phrase operated upon by the parsers is: How to V NG P NG P NG, where NG is a noun group or a pronoun, V is a verb, P is a preposition. Basing only on this formal representation, five possible variants of this phrase’s syntactic structure can be built, see Fig. 1.
A native speaker would choose the structure 4 as the most probable interpretation by taking into account some additional information, namely, lexical one. However, it is simple to give examples of phrases with the same basic structure How to V NG P NG P NG for that each of the other variants would be the correct one. Thus, a parser needs similar lexical information to disambiguate the phrase, i.e., to choose for this specific phrase one of the variants shown on Fig. 1.
There are many works devoted to this difficult problem; we can mention [3, 5, 9]. However, the problem is far from having being solved to an acceptable degree.
In our opinion, such a choice should be made in quantitative terms: we assign some weight, or a probability, to each variant; the more the weight the more sure we are that this variant is correct. Say, one variant can be assigned a weight 0.4 and another 0.6, then the latter variant is considered better than the first one. The quantitative character of the estimation allows for combination of different methods of disambiguation.
In this article, we will deal with the statistics of the combinations of individual words with prepositions[2]. Such combinations are similar to so-called subcategorization frames; we apply this notion to words of any part of speech. E.g., the tree number 1 on Fig. 1 contains only one non-trivial combination: put + in + on; the tree number 2 contains two such combinations: put + in, box + on, etc.
The choice of this type of combinations, namely, subcategorization frames, is not random, though we can’t discuss here the linguistic reasons for it. In short words, such combinations are to a good degree fixed for each specific word, so their statistics is more reliable than that of, say, arbitrary word pairs.
The proposed disambiguation method is based on the frequencies of such combinations both in phrases of the text and in the parser errors, i.e., in the trees generated by the parser, but rejected by human proof-readers or another disambiguation procedure, or absent in the training corpus such as the Penn TreeBank.
2. One-source generation and analysis model
In order to construct the formulae for statistical weights of the different variants of a phrase’s syntactic tree, basing on the subcategorization frames appearing in this tree, we will first consider a model of generation of phrases. In this section, a simplified and supposedly not sufficient model will be introduced; it will be improved in the next section.
|
1: How to [[[put the block] in the box] on the table]. 2: How to [[put [the block in the box]] on the table]. 3: How to [put [[the block in the box] on the table]]. 4: How to [[put the block] in [the box on the table]]. 5: How to [put [the block in [the box on the table]]]. Fig. 1. Hypothetical syntactic
structures for the sentence |
To simplify the reasoning by abstracting from the nature of the combinations of words with prepositions, we can formally consider all such combinations appearing in the syntactic tree of a phrase as some abstract features of the tree. We will number these features, e.g., a frame like “put + in + on” could be the feature number 1, “help + to” number 2, etc. We denote such features as f1, f2, etc. Let the full set, or dictionary, of these features be F.
Since
we are interested only in the statistics of the features fi (in our case the combinations) rather than in their
relationships, we will consider a phrase P just as a set of such features, P =
{![]() …,
…, ![]() }. E.g., we consider the phrase He speaks with the director of the institute about the plans as a
set P =
{he, speak + with + about, director
+ of, institute, plan}.
}. E.g., we consider the phrase He speaks with the director of the institute about the plans as a
set P =
{he, speak + with + about, director
+ of, institute, plan}.
To simplify the discussion, we suppose that each element can appear in a phrase only once, just ignoring multiple occurrences of the same combination, or feature, in one phrase. This allows us to consider a phrase as a simple set and also simplifies the model.
Let
us consider authoring of the text as a process of generation performed by some source S, like an apparatus that produces one by one some phrases![]() .
.
The model of generation is as follows. To generate a phrase P, the source S for each existing feature fi Î F decides whether or not this feature fi is to be included in the phrase P being generated. The decision is made randomly basing on the probability pi associated in the dictionary F with each feature fi. E.g., the generator S can include the feature “move + from + to” into each 1000th phrase P, then the corresponding pi = 0.001.
We assume that the features are included or not in P independently. Obviously, this contradicts to the idea of a coherent text generation: words in a phrase are not just random. However, we have to accept this assumption, because in the method of ambiguity resolution that we are discussing we suppose that there is no available knowledge of lexical co-occurrences, or lexical attraction [2, 10], and especially on co-occurrences of individual combinations. Since such knowledge involves statistics on pairs of combinations, that are very numerous, it would be difficult enough to extract it from a corpus with the necessary degree of reliability. Thus, we base our method on the only data set: the frequencies pi of individual combinations fi Î F.
Basing
on this knowledge and the independence hypothesis, we can calculate the frequency
of appearance of a specific phrase P = {![]() …,
…, ![]() } in the output of S.
Let qi = 1 – pi, and for this specific
phrase P suppose
} in the output of S.
Let qi = 1 – pi, and for this specific
phrase P suppose
![]() (1)
(1)
Obviously, the probability
P (P) =![]() , (2)
, (2)
since each feature fi independently is included in the phrase P with the probability pi or is not included with the probability qi.
Now we can make another assumption: The dictionary F of the features is so big that each specific feature fi is much more frequently absent in a phrase than present, i.e., pi » 0, qi » 1. This does correspond to the nature of the text: each word, except for some most common conjunctions and prepositions, that we do not consider in our discussion, appears in a minority of the phrases in the text. Thus, with some loss of precision, we can consider
P (P) »![]() ; (3)
; (3)
note that in this case the product is taken only by the elements of the phrase P, while in (2) it is taken by all the dictionary of features F.
The
formula (3) is much more convenient computationally than (2) since in this case
to calculate the probability of a specific phrase it is enough to fetch from
the dictionary F the frequencies pi for
each combination ![]() found in the phrase P,
without having to look through all the dictionary F. Because of this, we
will ignore the minor inaccuracy introduced by this equation.
found in the phrase P,
without having to look through all the dictionary F. Because of this, we
will ignore the minor inaccuracy introduced by this equation.
It
is possible to use this formula for disambiguation. Let us consider a set V ={V1, ¼,
![]() } of the variants of syntactic structure built by the
parser for the phrase P. Suppose exactly one of them is
correct (thus, we ignore the rare cases when no correct variant of syntactic
structure for the phrase can be built). Let Hj
be the hypothesis that the variant Vj
is correct. Let x
be the event of receiving exactly the set V as the parsing result. Then, by
the Bayes formula,
} of the variants of syntactic structure built by the
parser for the phrase P. Suppose exactly one of them is
correct (thus, we ignore the rare cases when no correct variant of syntactic
structure for the phrase can be built). Let Hj
be the hypothesis that the variant Vj
is correct. Let x
be the event of receiving exactly the set V as the parsing result. Then, by
the Bayes formula,
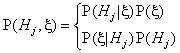
i.e.,
![]() (4)
(4)
For brevity, we will denote P (Hj | x) º Pj, the probability of that the variant Vj is the true one. Clearly,
![]() (5)
(5)
since exactly one variant is true. Thus, we can ignore all the factors that are common for the expressions for all the Hj. Now we will consider these factors.
Since the event x does not depend on j at all, we also can ignore it. Suppose we have a priori no information about the probabilities of individual hypotheses that would be based just on the trees Vj without their comparison with each other. Then we can ignore the factor P (Hj) in (4). Thus, (4) can be rewritten as
Pj ~ P (x | Hj), (6)
where ~ means proportional, i.e., Pj = C ´ P (x | Hj) with a normalizing constant C determined from (5). Clearly, if we have any a priori information about the probability of individual variants Vj based on, say, mean length of syntactic links or probabilities of the corresponding grammar rules, etc. [8], we can keep the factor P (Hj) in (6).
Let’s calculate the value of P (x | Hj). Thus, we suppose that the hypothesis Hj is true, i.e., that Vj = P and all the other variants Vk, k ¹ j, are the noise. Suppose the noise gets into the set V independently of the true structure of P. This is clearly not correct, but in our case we consider that we don’t have any useful information about the nature of their dependency. Then, since Vj = P,
P (x | Hj) = P (P) ´ P (V / Vj), (7)
where P (V / Vj) is the noise, the set of all the incorrect variants of the structure generated by the parser.
The meaningful discussion of this equation will be present in the next section. Now we will try to make a simple but, in our opinion, wrong assumption about this equation.
Suppose the noise in (7) is a white noise, i.e., the probability of any set of such noise variants is the same (in the next section we will show how to avoid this assumption). Then we can ignore the factor P (V / Vi) in (7) and finally get Pj ~ P (P) and by (6), (7), and (3)
Pj ~ ![]() , (8)
, (8)
i.e., to calculate the probability, or weight, of the j-th variant of analysis, the frequencies of all the features found in it should be fetched from the dictionary and multiplied. Such weights should be normalized by the set V. The best value of the weight corresponds to the most probable variant of the structure. In the process of analysis, this best variant should be accepted and considered true, and all the others should be rejected.
Of course the equation (8) is well known and intuitively clear: in everyday life, people judge about the probabilities of different variants of, say, radio news by frequencies of the corresponding events. However, in the next section we will show how to improve it if we have a little bit more information about our parser.
3. Two-source generation and analysis model
In the previous section, one of the assumptions was that any set of noise variants has the same probability to appear in the parser output V: P (V / Vj) = P (V / Vk) for all i, k £ |V|. Now we will discuss the situation when this is not the case.
As in the previous section, consider that the phrases like P are generated by some source S+ of the correct phrases. The noise variants of analysis are generated by some source S– of errors.
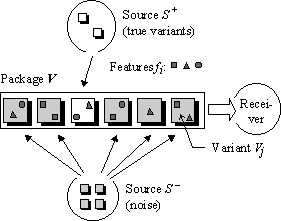
Fig. 2. Two-source model of generation of the parsing results.
We
can model the process of analysis as follows, see Fig. 2. A package V
of elements (sets Vj of
features fi) is generated
by the two sources, S+ and
![]() Only one element of V
(the true variant) is generated by
the source S+, and all the
others by
Only one element of V
(the true variant) is generated by
the source S+, and all the
others by ![]() Thus, the disambiguation
module receives such a package V, and its task is to guess which
one element of V was generated by S+.
The decision is made basing on the features fi
found in each of the elements.
Thus, the disambiguation
module receives such a package V, and its task is to guess which
one element of V was generated by S+.
The decision is made basing on the features fi
found in each of the elements.
Suppose
we have a statistics on the frequencies of individual features in the elements
generated by S+ and ![]() Namely, in the
variant being generated, S+
includes a feature fi with
the frequency
Namely, in the
variant being generated, S+
includes a feature fi with
the frequency ![]() , and S–
with the frequency
, and S–
with the frequency ![]() .
.
Suppose the variants generated by the source S– are independent from each other and are independent from the variant generated by S+ (clearly in reality this is not the case, but we still do not have any useful information on the character of their interdependencies).
Let’s
return to the equation (7). The hypothesis Hj
is equivalent to the assertion that the variant Vj was generated by the source S+, while all the other variants by ![]() Let P+ (x) be the frequency of generation of
some set x of elements by the source S+, and P– (x) by
Let P+ (x) be the frequency of generation of
some set x of elements by the source S+, and P– (x) by ![]() Then we can rewrite
(6) and (7) as
Then we can rewrite
(6) and (7) as
Pj ~ P+ (Vj) ´ P– (V / Vj). (9)
Let’s apply the independence hypothesis for S– and then perform some purely arithmetical transformations (note the change of V / Vj to V in the 4th line):
|
Pj |
~ P+ (Vj) ´ P– (V / Vj) |
|
|
= P+ (Vj) ´
|
|
|
= P+ (Vj)
´ |
|
|
= |
In
the 3rd line, the right part of the equation was multiplied and
divided by the same value, and in the 4th line the numerator of this
fraction was introduced into the product. Since the factor![]() does not depend on j,
by the normalizing condition (5) we can ignore it, and then by independence
hypothesis and by equation (3) substitute the probabilities for the products of
pi:
does not depend on j,
by the normalizing condition (5) we can ignore it, and then by independence
hypothesis and by equation (3) substitute the probabilities for the products of
pi:
Pj ~
![]() =
= 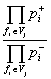 =
= 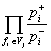 .
.
Finally we get
Pj ~ 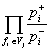 . (10)
. (10)
Thus,
to calculate the weight of the j-th
variant, the frequencies ![]() and
and ![]() of all the features fi found in this variant Vj should be fetched from the
dictionary F, and their quotients multiplied.
of all the features fi found in this variant Vj should be fetched from the
dictionary F, and their quotients multiplied.
Two
minor problems connected to the equation (10) need some clarification, namely,
the problems arising when ![]() = 0 or
= 0 or ![]() = 0.
= 0.
First problem:
![]() = 0. The equation (10) seems to contain a logical
contradiction since if
= 0. The equation (10) seems to contain a logical
contradiction since if ![]() = 0 it causes a zero division. In fact, this spurious
contradiction was introduced artificially at the 3rd line of
the process of simplifying the equation
(9) above, by simultaneous multiplication and division by P– (Vj), that in this case proves
to be zero. If we instead represent the equation (10) in the equivalent form
(11) by immediate application of the equation (3) to the equation (9):
= 0 it causes a zero division. In fact, this spurious
contradiction was introduced artificially at the 3rd line of
the process of simplifying the equation
(9) above, by simultaneous multiplication and division by P– (Vj), that in this case proves
to be zero. If we instead represent the equation (10) in the equivalent form
(11) by immediate application of the equation (3) to the equation (9):
Pj =
![]() ´
´
![]() , (11)
, (11)
(the
expression contains a product of products since V is a set of sets Vk of features fi) then the contradiction
disappears. In any case that caused a zero division in (10), the corresponding
expression (11) just does not contain the offending value ![]() for the fi Î Vj
since Vj is excluded from
the second product. Thus, there is no contradiction in the expression (10).
for the fi Î Vj
since Vj is excluded from
the second product. Thus, there is no contradiction in the expression (10).
What
is more, in practice there is no need to use the equation (11) as a special
case for ![]() = 0, since the equation (10) can be used in all cases in
the modified form (12) which will be discussed in the next section.
= 0, since the equation (10) can be used in all cases in
the modified form (12) which will be discussed in the next section.
Second problem:
![]() = 0. This problem is connected with the case when the
phrase contains a word that was never encountered previously in the training
data. Obviously for any combination fi
containing such a word,
= 0. This problem is connected with the case when the
phrase contains a word that was never encountered previously in the training
data. Obviously for any combination fi
containing such a word, ![]() = 0. Then Pj = 0
for all j, that contradicts to the
normalizing condition (5).
= 0. Then Pj = 0
for all j, that contradicts to the
normalizing condition (5).
To
solve this problem, it would look natural to make the decision basing on the
number of the zeroes in the expression (10): the best variant should contain
the minimal number of unknown combinations. Namely, all the variants that have
more than the minimal number of zeroes in the expression should be assigned a
zero weight, and for the rest of the variants, the zero factors ![]() should be removed
from the expression (10). Then they should be compared normally.
should be removed
from the expression (10). Then they should be compared normally.
For example, if P1 ~ 0 ´ 0 ´ 0.3, P2 ~ 0 ´ 0.7 ´ 0.3, and P3 ~ 0 ´ 0.5 ´ 0.2, then P1 = 0, so V1 should be rejected, and the expressions for P2 and P3 should be compared without the zeroes: P2 ~ 0.7 ´ 0.3 = 0.21, P3 ~ 0.5 ´ 0.2 = 0.20, so V2 is the best.
In
practice, instead of introducing a special case for ![]() = 0, we use some very small number e <<
1, say, e =
10-10, i.e., when
= 0, we use some very small number e <<
1, say, e =
10-10, i.e., when ![]() = 0, we use
= 0, we use ![]() = e,
and the same for
= e,
and the same for![]() . This does not introduce any significant inaccuracy, but
allows to normally use the expression (10), in the form (12), in all cases.
. This does not introduce any significant inaccuracy, but
allows to normally use the expression (10), in the form (12), in all cases.
However,
in connection with the problem of ![]() = 0 or
= 0 or ![]() = 0, usually corresponding to some very rare words or
constructions, we should mention that in our experiments these rare features
led to some instability of the model. This issue will be discussed in the
section 5.
= 0, usually corresponding to some very rare words or
constructions, we should mention that in our experiments these rare features
led to some instability of the model. This issue will be discussed in the
section 5.
The equation (10) is intuitively clear as well: in everyday life, people trust some radio news and do not trust other basing on both probabilities of the corresponding events and the frequency of the radio agencies lying (well, making errors) on a specific type of subjects.
4. Some examples
Let’s
consider some examples of application of the discussed method. Since the
principal point of the article is the idea that taking into account the values ![]() improves the accuracy
of disambiguation, in each example we will compare the results obtained with
the expressions (8) and (10).
improves the accuracy
of disambiguation, in each example we will compare the results obtained with
the expressions (8) and (10).
Example 1. Let us first consider a simple example from another application, namely, from part of speech disambiguation.
Suppose
the frequencies of different parts of speech in the texts under investigation
are: ![]() = 0.4,
= 0.4, ![]() = 0.4,
= 0.4, ![]() = 0.2. Let the part of speech tagger we use sometimes
erroneously reports some additional variants for words. If this is all the information
we have, then, given the result of the analysis V = {{adjective}, {verb}} (where each variant consists of only one feature: V1 = {adjective}, V2 = {verb}),
we would reason like this: Since
= 0.2. Let the part of speech tagger we use sometimes
erroneously reports some additional variants for words. If this is all the information
we have, then, given the result of the analysis V = {{adjective}, {verb}} (where each variant consists of only one feature: V1 = {adjective}, V2 = {verb}),
we would reason like this: Since ![]() >
>![]() , then the correct variant should be adjective, namely, by the equations (8) and (5), its weight is
P ({adjective}) =
0.4 / (0.4 + 0.2) » 0.66 while the weight P ({verb}) = 0.2 / (0.4 +
0.2) » 0.33.
, then the correct variant should be adjective, namely, by the equations (8) and (5), its weight is
P ({adjective}) =
0.4 / (0.4 + 0.2) » 0.66 while the weight P ({verb}) = 0.2 / (0.4 +
0.2) » 0.33.
Given another set of the results V = {{noun}, {adjective}}, the weights are P ({noun}) = P ({adjective}) = 0.5, so no decision can be made.
Suppose now that we know that the part of speech tagger we use reports erroneously a noun with the frequency 0.9, an adjective with the frequency 0.1, and has never reported a verb erroneously. The difference might result from, say, some context analysis it performs. Then, in the same case of V = {{adjective}, {verb}}, we can say definitely that verb is the correct answer, since the parser never makes an error of misreporting a verb.
In the second case, that of V = {{noun}, {adjective}}, according to (10) we calculate the weights as
|
P ({noun}) |
~ 0.4 / 0.9 » 0.44, |
|
P ({adjective}) |
~ 0.4 / 0.1 » 4.00, |
and after normalization by (5), P ({noun}) = 0.44 / (0.44 + 4.0) » 0.1, P ({adjective}) » 0.9, thus, in this case we are almost sure that the correct answer is adjective. Note the difference with the results of the previous example.
Example 2. This is a little bit artificial example from syntax. Let’s consider a text corpus consisting of the following three phrases:
1. He spoke with the director about the plan.
2. He spoke with the director of the institute.
3. He spoke with my colleagues of the plan.
For each phrase, two variants of analysis are built, e.g., for the first one: V ={V1, V2}, V1 = {speak + with, director + about}, V2 = {speak + with + about, director}. In fact, V2 is the correct one.
By this corpus we can build the following dictionary F of combinations (for convenience, in the columns p+ and p– we show the number of occurrences instead of frequencies):
|
|
|
|
|
Feature f |
p+ |
p– |
|
speak + with + about |
1 |
0 |
|
speak + with + of |
1 |
1 |
|
speak + with |
1 |
2 |
|
director + about |
0 |
1 |
|
director + of |
1 |
0 |
|
director |
1 |
1 |
|
colleague + of |
0 |
1 |
|
colleague |
1 |
0 |
|
he |
6 |
0 |
|
plan |
4 |
0 |
|
institute |
2 |
0 |
Now,
let us consider a phrase like He spoke
with my brother of his job. The parsing results V ={V1, V2}, V1 = {speak + with, brother + of}, V2 = {speak + with + of, brother}. Since there was no phrase with
the word brother in the training
corpus, in both variants one factor will be zero or, as we have decided above,
an e <<
1: ![]() =
= ![]() = e;
= e;
![]() =
= ![]() = e.
Then, by normalizing condition (5), these factors can be ignored.
= e.
Then, by normalizing condition (5), these factors can be ignored.
If we use only the expression (8), we get
P1 ~ ![]() ~ 1,
~ 1,
P2 ~ ![]() ~ 1,
~ 1,
so the two variants can’t be distinguished. However, with the expression (10),
P1 ~ 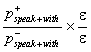 ~ 0.5,
~ 0.5,
P2 ~ 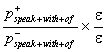 ~ 1.0,
~ 1.0,
so in this case the latter variant should be chosen. Clearly, this example is only an illustration of the computational procedure. In reality, a large enough corpus should be used to train the model. Also, the method is useful for sophisticated enough parsers (grammars) with complex behavior.
5. Experimental results
This work is a part of a larger project on automatic extraction of a dictionary of subcategorization frames from a large text corpus [6, 7]. For the reasons connected with that larger project, the experiments were conducted on an artificially generated set of quasi-sentences. The method described in the article was a part of an iterative re-estimation procedure used for disambiguation of this corpus.
In the experiments, the results of disambiguation using the expression (12) were always better than the results obtained with the expression (8). The difference was no very big, though. The typical results were as follows: with the method (12), the procedure reported incorrectly 14% of ambiguous sentences, while with the method (8), the error rate was 21%. Only ambiguous sentences were taken into account; and the whole tree was considered correct or not, rather than individual nodes or links.
At the moment, we are in the final stage of preparation for experiments with a real text corpus. We hope that by the time of the Symposium the results will be known.
One significant detail was found empirically during the experiments. The results were more stable and the error rate was significantly lower, when we suppressed the very rare cases, i.e., the features with very low frequency, by artificially adding some additional noise. The best results were obtained with the following expression:
Pj ~ 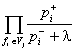 , (12)
, (12)
where
l »![]() , S is the number
of sentences in the corpus, and V is
the total number of the variants generated for the corpus by the parser. Thus the
expression for l
is the quotient of the number of correct and incorrect variants built by the
parser. For the moment we can’t give a good explanation of the empirical fact
that this value of l
proves to be optimal.
, S is the number
of sentences in the corpus, and V is
the total number of the variants generated for the corpus by the parser. Thus the
expression for l
is the quotient of the number of correct and incorrect variants built by the
parser. For the moment we can’t give a good explanation of the empirical fact
that this value of l
proves to be optimal.
6. Conclusions and future work
As it was shown, taking into account the frequencies of the specific parsing errors made by a specific parser used in the system, can improve the accuracy of disambiguation of the results of analysis: In everyday life, people trust radio news basing on both probabilities of the events and the frequency of the radio agencies lying on a specific type of subjects. In short words, the main idea of the article is that the equation (10) performs better than (8).
The described method of disambiguation can be applied to sophisticated parsers or grammars, for which it is difficult to predict, or explain the reasons for, their errors, so that the only thing that can be done is statistical analysis of the observed behavior of the parser.
The method is based on the following data stored in the dictionary:
· The
frequencies ![]() of the individual
features of the structure under investigation (characteristics; in our case,
combinations of words with prepositions) in the correct phrases, i.e., in the text itself, in language;
of the individual
features of the structure under investigation (characteristics; in our case,
combinations of words with prepositions) in the correct phrases, i.e., in the text itself, in language;
· The
frequencies ![]() of these features in
the incorrect variants of analysis,
i.e., in the parsing errors.
of these features in
the incorrect variants of analysis,
i.e., in the parsing errors.
In disambiguation process, the weights of the variants of the structure can be calculated as
Pj ~ 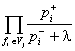 , (12)
, (12)
and the variant with the largest weight should be accepted. If there is any a priori information on the probabilities of the corresponding variants, based on the properties of their nodes, links, etc., then the right part of (12) can be multiplied by the corresponding factors P (Hj); see the discussion after the equation (6).
The model can be trained on an existing corpus with marked up syntactic structures, such as the Penn TreeBank. To train the model, the corpus is processed by the parser used in the system, and the information on the occurrences of the combinations (features) in the correct and false variants is accumulated in the dictionary. We have also proposed an iterative re-estimation procedure that allows to use just raw data to train the model [6].
In our opinion, this method can be applied to a wide range of disambiguation tasks, such as:
· Part of speech tagging (we have discussed a corresponding example),
· Statistical grammars [1, 8],
· Lexical attraction disambiguation schemes [2, 10].
However, some parts of our reasoning seems to be not clear enough and need further investigation. First of all these are our independence hypotheses. The method is based on a set of such hypotheses, of which two are most important:
1. The errors connected with misreporting of specific combinations (generally, features of the variants) are introduced in the analysis results independently of the correct structure of the phrase (or, better to say, we have no useful quantitative data on such dependencies, or we can’t store such data in the dictionary due to its too large amount);
2. The errors connected with individual features are introduced in the variants of the analysis results independently from each other (again, it’s better to say that we have no available useful quantitative data on such dependencies);
These
two hypotheses allow us to use the expressions like ![]() for the probabilities
of the variants Vj, not
taking into account the dependencies between the variants Vk nor between them and the phrase P.
for the probabilities
of the variants Vj, not
taking into account the dependencies between the variants Vk nor between them and the phrase P.
These hypotheses are weak links in our reasoning, but we have to accept them unless the corresponding data is available. Clearly, in reality there should be some dependencies between the variants of the structure of the same phrase. We think that further investigation of such dependencies may shed more light on statistical disambiguation and improve our method.
Another weak link is the use of the constant l in (12) to smooth the effect of rare cases. It is not clear whether this method is good and whether there are better ways. The specifics of language data is that the rare cases are the most frequent ones. Thus, the ways should be investigated to use these data instead of suppressing them. This is work for the future.
References
5. Collins, M., and J. Brooks. Prepositional phrase attachment through a backed-off model. Proc. of the Third workshop on very large corpora, 30 June 1995, MIT, Cambridge, Massachusetts, USA.
6. Gelbukh, A.F., I.A. Bolshakov, and S.N. Galicia-Haro. Automatic learning of a syntactical government patterns dictionary from Web-retrieved texts. Proc. of CONALD-98, Pittsburgh, PA, 1998.
7. Gelbukh,
A.F., I.A. Bolshakov, and S.N. Galicia-Haro. Syntactic disambiguation
by learning weighted government patterns
from a large corpus. Technical report, CIC, IPN, Mexico, 1998 (to appear).
8. Goodman, Joshua T. Parsing inside-out. Ph.D. thesis, Harvard University, Cambridge, MA, 1998. See http://xxx.lanl.gov/abs/cmp-lg/9805007.
10.Yuret, Deniz. Discovery of linguistic relations using lexical attraction. Ph.D. thesis, MIT, 1998. See http://xxx.lanl.gov/abs/cmp-lg/9805009.